NMR in Strongly Correlated Electron System

• HOME
• RESEARCH
• MEMBER
• LABOLATORY
• PUBLICATION
• ACCESS

　　　　SUPERCONDUCTIVITY　　　　　 FRUSTRATION　　　　 HIGH PRESSURE NMR　　　　 ORBIAL

■ FRUSTRATION

■ Heptamer vs heavy fermion

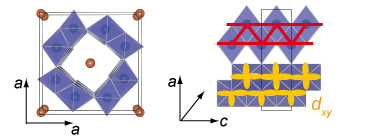
Pyrochlore lattice has the strongest frustration and hence can give quantum spin liquid as the ground state of antiferromagnetically-coupled localized spins. The macroscopic degeneracy of the ground state is highlighted in the diversity of magnetism.
Spinel oxides having the V pyrochlore lattice are interesting in that the geometric frustration is imposed on the spin, charge, and orbital degrees of freedom. Especially interesting materials are AlV₂O₄ and LiV₂O₄. AlV₂O₄ has 3d^2.5 electrons and insulating ground states. Our NMR measurements uncovered the unusual magnetic ground state with the nonmagnetic heptamer and magnetic triangular lattice, which have been proposed theoretically. In contrast, LiV₂O₄ having 3d^2.5 electrons is metal with the effective mass 1000 times heavier than that of free electron. Many origins have been theoretically proposed; geometric frustration, orbital fluctuations, strong correlation, etc. To give microscopic insight, we have revealed the 3d orbital state from the anisotropy of magnetic hyperfine coupling.

■ Trimer vs tetramer

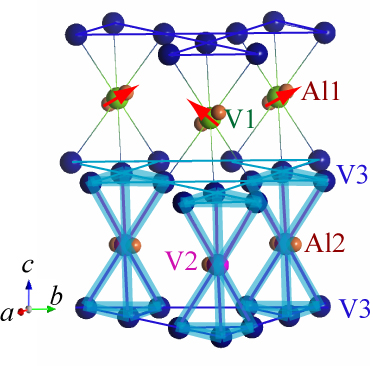
Triangular lattice is the typical example of two-dimensional frustrated lattice. In presence of orbital degrees of freedom, the ways of symmetry breaking can be diverse; nonmagnetic trimer and dimer, magnetic tetramer and trimer, etc. We revealed the local spin and orbital states in the bilayer triangular lattice system BaV₁₀O₁₅.

■ Peierls vs Mott

Peierls transition and Mott transition are contrasting basic notions of metal-insulator transition. They are hardly distinguishable in the quasi-one-dimensional system with strong electron correlation, as discussed in VO₂. In a V hollandite K₂V₈O₁₆ having zigzag ladders, these two features are competes with each other owing to the geometric frustration, which is evidenced from the coexistence of nonmagnetic and paramagnetic V sites observed by ⁵¹V NMR at ambient pressure and under pressure. The pressure-temperature phase diagram based on 1/T₁ and 1/T₂ measurements suggests that the transition is Mott like at low pressures and becomes more Peierls like at high pressure.